[시계열 분석]R에서 ACF와 PACF를 활용한 정상성(Stationary) 확인

정상성을 확인하기에 앞서 시도표(time plot)을 그려봅니다. r에서 제공하는 기본함수만 사용하더라도 time plot을 쉽게 그릴 수 있습니다.

R에서 ts()함수

ts()함수에 매트릭스나 벡터를 입력해주면, 시계열 데이터로 변환합니다. 여기서 start=c(2006,1)은 2006년 1분기부터 시작됨을 뜻합니다. frequency=4는 년도별 총 4개의 분기가 존재함을 뜻합니다.

• Random variation Time Series

dd1 <- matrix(c(1342, 1442, 1252, 1343, 1425, 1362, 1456, 1272, 1243,
1359,1412, 1253, 1201, 1478, 1322, 1406, 1254, 1289, 1497, 1208))
dd1.ts <- ts(data=dd1, start=c(2006,1), frequency=4)
dd1.ts

##      Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1342 1442 1252 1343
## 2007 1425 1362 1456 1272
## 2008 1243 1359 1412 1253
## 2009 1201 1478 1322 1406
## 2010 1254 1289 1497 1208

• Seasonal variation Time Series

dd2 <- matrix(c(1142, 1242, 1452, 1543, 1125, 1262, 1456, 1572, 1143, 1259,
1462, 1553, 1121, 1258, 1472, 1546, 1154, 1249, 1477, 1548))
dd2.ts <- ts(data=dd2, start=c(2006,1), frequency=4)
dd2.ts

##      Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1142 1242 1452 1543
## 2007 1125 1262 1456 1572
## 2008 1143 1259 1462 1553
## 2009 1121 1258 1472 1546
## 2010 1154 1249 1477 1548

• Trend variation Time Series

dd3 <- matrix(c(1142, 1242, 1252, 1343, 1225, 1562, 1356, 1572, 1343, 1459,
1412, 1453, 1401, 1478, 1322, 1606, 1554, 1589, 1597, 1408))
dd3.ts <- ts(data=dd3, start=c(2006,1), frequency=4)
dd3.ts

##      Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1142 1242 1252 1343
## 2007 1225 1562 1356 1572
## 2008 1343 1459 1412 1453
## 2009 1401 1478 1322 1606
## 2010 1554 1589 1597 1408

• Trend and Seasonal variation Time series

dd4 <- matrix(c(1142, 1242, 1452, 1543, 1225, 1362, 1556, 1672, 1343, 1459,
1662, 1753, 1421, 1558, 1772, 1846, 1554, 1649, 1877, 1948))
dd4.ts <- ts(data=dd4, start=c(2006,1), frequency=4)
dd4.ts

##      Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1142 1242 1452 1543
## 2007 1225 1362 1556 1672
## 2008 1343 1459 1662 1753
## 2009 1421 1558 1772 1846
## 2010 1554 1649 1877 1948

• Cyclinical variation Time Series

dd5 <- matrix(c(1142, 1242, 1452, 1543, 1225, 1362, 1556, 1672, 1343, 1459,
1662, 1753, 1221, 1358, 1572, 1646, 1154, 1249, 1477, 1548))
dd5.ts <- ts(data=dd5, start=c(2006,1), frequency=4)
dd5.ts

##      Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1142 1242 1452 1543
## 2007 1225 1362 1556 1672
## 2008 1343 1459 1662 1753
## 2009 1221 1358 1572 1646
## 2010 1154 1249 1477 1548

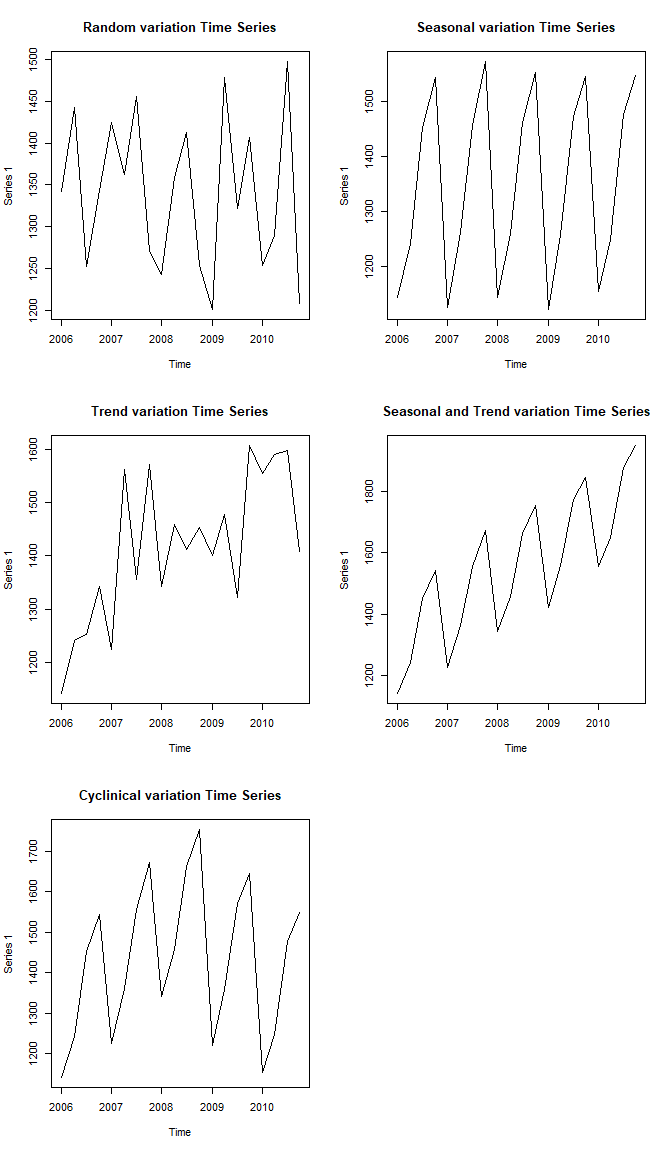
시도표(time plot)

r의 기본함수 plot()과 ts()를 사용하여 time plot을 그릴 수 있습니다.

par(mfrow=c(3,2))
plot(dd1.ts, main='Random variation Time Series')
plot(dd2.ts, main='Seasonal variation Time Series')
plot(dd3.ts, main='Trend variation Time Series')
plot(dd4.ts, main='Seasonal and Trend variation Time Series')
plot(dd5.ts, main='Cyclinical variation Time Series')

ACF와 PACF

ACF와 PACF는 시계열 정상성 여부를 판달할 때 뿐만 아니라, 모형식별에서도 사용합니다. 모형식별을 위한 ACF와 PACF사용은 추후에 다뤄보겠습니다. 여기서는 정상성 유무만을 판단하기 위해 ACF와 PACF를 사용합니다. 정상성을 가지는 대표적인 예로 백색잡음(white Noise)이 있고, 비정상성을 가지는 예로 확률보행(Random Walk)이 있습니다. 이 둘의 표본을 생성하여 ACF와 PACF를 비교해봅니다.

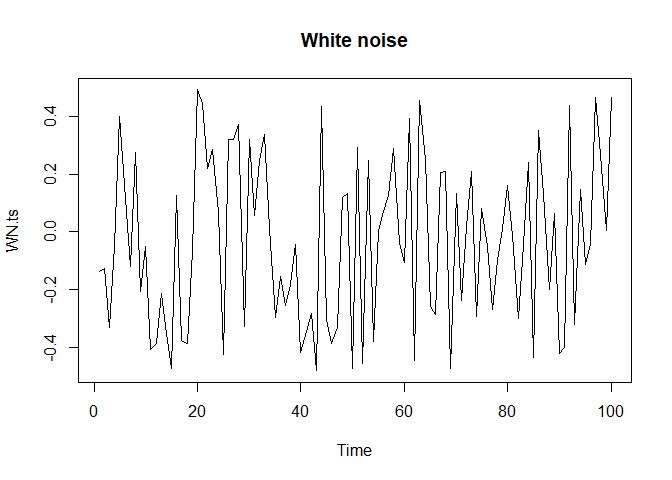
1.1 White Noise 우선 White Noise를 생성한 후, time plot을 그립니다.

WN <- runif(100, min = -0.5, max = 0.5)
WN.ts <- ts(data=WN, start=c(1,1),frequency = 1)
plot(WN.ts, mai="White noise")

1.2 ACF & PACF of White Noise

par(mfrow=c(1,2))
acf(WN.ts, main="ACF")
pacf(WN.ts, main="PACF")

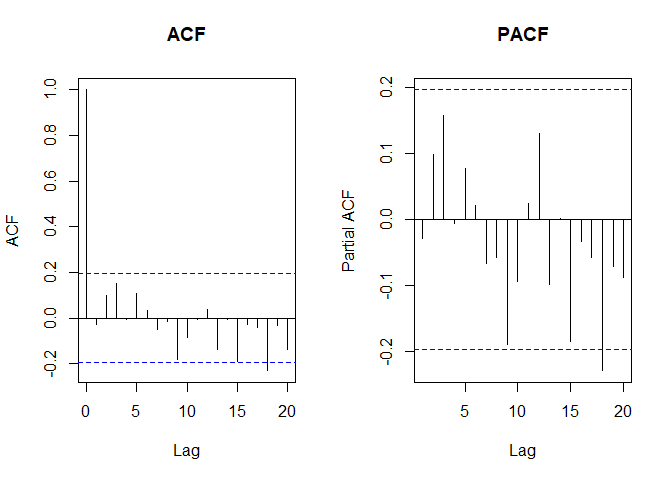
• ACF의 x축은 시차(lag), y축은 autocorrelation
• PACF의 x축은 시차(lag), y축은 partial autocorrelation
• 시차가 0일 때, autocorrelation은 항상 1의 값을 가집니다.
• 대부분 값들이 파란선 내부에 위치한 것으로 보아 정상성을 가짐을 유추할 수 있습니다.

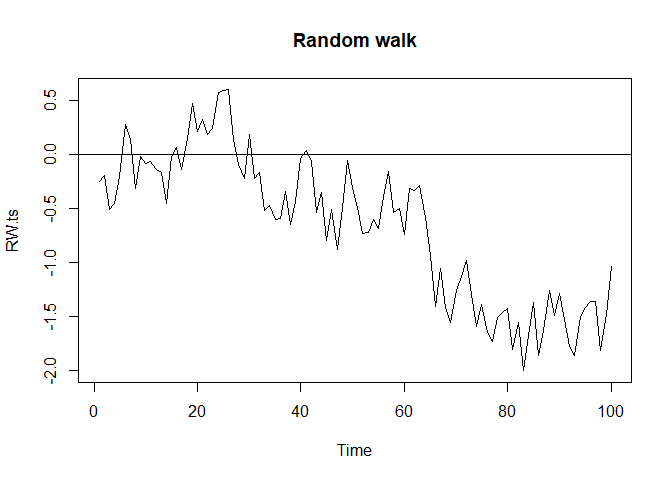
2.1 Random Walk random walk로부터 표본을 생성 후, time plot을 그립니다.

at <- runif(100, min=-0.5, max=0.5)
yt <- runif(100, min=-0.5, max=0.5)
#난수 생성
for(i in 2:100){yt[i] = yt[i-1] + at[i]}

RW.ts <- ts(data=yt)
plot(RW.ts, main="Random walk")
abline(h = 0)

1.2 ACF & PACF of Random Walk

par(mfrow=c(1,2))
acf(RW.ts, main="ACF")
pacf(RW.ts, main="PACF")

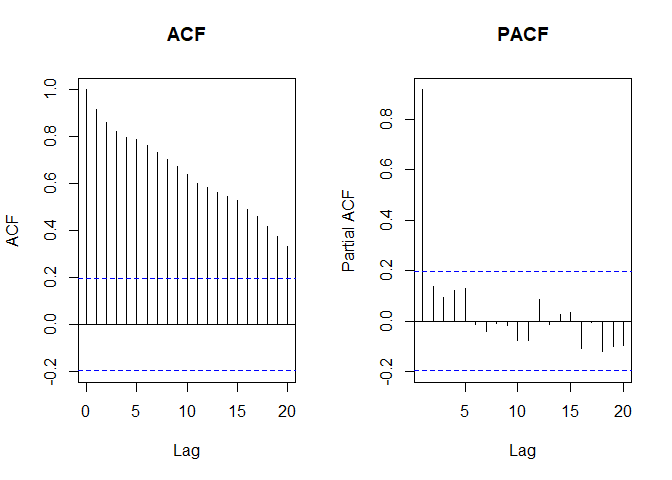
• ACF의 값들이 파란선에서 크게 벗어납니다. 따라서 비정상 시계열임을 유추할 수 있습니다.

정상성 검정하기에 앞서 단지 시각적으로 확인했을 뿐입니다. 정상성 혹은 비정상성이라고 결론을 내리기엔 아직 섣부릅니다.

KPSS test

tseries패키지의 kpss.test함수를 사용하여, null="Level"옵션을 지정하면 정상성 검정이 가능합니다. 여기서 귀무가설 H0는 “정상성을 만족한다.” 입니다.

1. White Noise일 때, 정상성 검정

tseries::kpss.test(WN.ts, null = "Level")

## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo

## Warning in tseries::kpss.test(WN.ts, null = "Level"): p-value greater than
## printed p-value

## 
##  KPSS Test for Level Stationarity
## 
## data:  WN.ts
## KPSS Level = 0.11076, Truncation lag parameter = 4, p-value = 0.1

• p-value는 아주 큰 값을 가집니다.
• 따라서 “정상성을 만족한다”는 귀무가설을 기각하지 못합니다.

1. Random Walk일 때, 정상성 검정

tseries::kpss.test(RW.ts, null = "Level")

## Warning in tseries::kpss.test(RW.ts, null = "Level"): p-value smaller than
## printed p-value

## 
##  KPSS Test for Level Stationarity
## 
## data:  RW.ts
## KPSS Level = 1.7658, Truncation lag parameter = 4, p-value = 0.01

• p-value는 아주 작은 값을 가집니다.
• 따라서 “정상성을 만족한다”는 귀무가설을 기각합니다.